Come fanno gli aerei a volare? L’origine della portanza spiegata

Se vi siete mai chiesti come fanno gli aerei a volare, probabilmente avrete anche già provato a cercare qualche delucidazione sull’origine della portanza – la forza che permette ad un corpo di librarsi in aria – e avrete notato che è piuttosto facile imbattersi in spiegazioni differenti. Infatti, per cercare di chiarire in modo semplice come facciano gli oggetti a volare spesso si ricorre a svariate teorie che non sono in grado di giustificare appieno tutti gli aspetti della fisica del volo, sebbene possano essere usate proficuamente per comprenderne alcuni elementi. Due argomenti molto comuni in questo senso sono la giustificazione della portanza tramite l’equazione di Bernoulli e il terzo principio della dinamica – quest’ultimo detto anche di azione-reazione.

Le equazioni di Navier-Stokes

Dare una spiegazione onnicomprensiva sull’origine della forza che permette il volo non è un compito semplice, perché essa è il risultato di una mutua interazione fra il corpo immerso nel fluido e il fluido stesso. In questo articolo cercheremo di illustrare l’origine della portanza andando a cercare la risposta direttamente nelle equazioni che governano il moto dei fluidi: le celebri equazioni di Navier-Stokes, così chiamate in onore del matematico irlandese George G. Stokes e dell’ingegnere francese Claud-Louis Navier che le teorizzarono nel corso del XIX secolo.

Per comprendere nel dettaglio la formulazione matematica delle equazioni di Navier-Stokes è necessario avere una conoscenza di livello accademico. C’è però da dire che il principio cardine alla loro base si fonda su un concetto che si affronta già alle scuole superiori: la seconda legge di Newton. Perciò, giusto per avere un’idea perlomeno intuitiva di quale sia il significato fisico delle equazioni di Navier-Stokes, possiamo semplicemente pensarle come l’applicazione del secondo principio della dinamica ad un fluido: forza uguale massa per accelerazione.

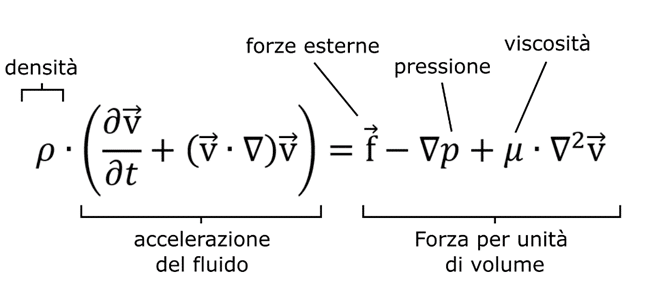
Ovviamente, la natura delle equazioni di Navier-Stokes è molto complicata dal momento che devono descrivere un fenomeno così complesso come il moto di un fluido. D’altronde, non bisogna certo essere degli scienziati per rendersi conto di quanto difficile possa essere modellare matematicamente il comportamento di una sostanza che può scorrere e mescolarsi in modo caotico. Giusto per darvi un’idea di quanto questa formulazione sia tanto importante quanto complicata, sappiate che il Clay Mathematics Institute ha inserito la risoluzione delle equazioni di Navier-Stokes fra i sette problemi matematici del millennio per la cui soluzione vi è un premio da un milione di dollari. Ad oggi, infatti, non esistono soluzioni analitiche – ottenibili con carta e penna per intenderci – alle equazioni di Navier-Stokes se non per casi molto semplici e di limitato interesse industriale.

Per nostra fortuna però, una soluzione approssimata di tali equazioni – che diventa tanto più precisa quanta più potenza di calcolo si ha a disposizione – può essere ottenuta grazie a moderni software di modellazione fisica basati sulla cosiddetta Computational Fluid Dynamics. Oggigiorno non c’è applicazione avanzata che riguardi i fluidi che non si appoggi alla CFD: analisi aerodinamica delle automobili, aerodinamica dei velivoli, modelli metereologici, analisi dei flussi di sangue nel sistema cardiocircolatorio e chi più ne ha più ne metta.

Da dove nasce la portanza

Dopo aver adeguatamente introdotto le equazioni di Navier-Stokes, possiamo passare alla spiegazione sull’origine della portanza e come promesso lo faremo risolvendo direttamente tali equazioni tramite CFD. Generalmente, per analizzare l’interazione fra l’aria e l’ala di un aeroplano si parte in prima istanza dal suo profilo alare, ovvero una semplice sezione dell’ala. Per questo esempio abbiamo scelto un profilo alare simmetrico standard (NACA 0018), uno dei tanti sviluppati e standardizzati dalla NACA – l’antenata della NASA odierna – durante la prima metà del Novecento.

Se vi ricordate, all’inizio dell’articolo abbiamo detto che la portanza nasce dalla mutua interazione fra l’ala e l’aria che le fluisce attorno. Sostanzialmente, quello che succede è che la presenza dell’ala modifica localmente il percorso dell’aria e le quantità ad essa associate – leggasi velocità e pressione. Quando il campo di pressione sopra e sotto l’ala non è simmetrico si ottiene una forza netta – detta appunto portanza – che spinge l’ala verso l’alto in risposta al “disturbo” provocato da quest’ultima al flusso d’aria.

In realtà, non è solo la differenza in termini di pressione a generare la portanza, ma anche gli effetti viscosi dell’aria, i quali però hanno un impatto molto minore e possono essere spesso trascurati come vedremo in seguito. Consideriamo subito il caso in cui il profilo alare è perfettamente allineato rispetto alla direzione del vento che incontra: proprio come ci aspettavamo, i risultati della simulazione CFD mostrano un campo variabile di pressione tutto intorno all’ala a causa della sua interazione con l’aria circostante. Tuttavia, la portanza sul profilo alare risulta nulla.

Ciò accade perché il campo di pressione è simmetrico rispetto al profilo alare e quindi non esiste una vera differenza di pressione netta fra il dorso e il ventre dell’ala che possa spingerla verso l’alto. Viceversa, se consideriamo i risultati per lo stesso profilo nelle medesime condizioni, ma inclinando leggermente la direzione del vento – che è come dire che l’ala sia leggermente inclinata verso l’alto, un po’ come avviene durante un decollo – si ottiene della portanza. In quest’altro caso, sotto l’ala si sviluppa una regione a pressione (relativa) positiva – ovvero localmente la pressione è più alta di quella atmosferica – mentre sopra si sviluppa una regione a pressione (relativa) negativa. Intuitivamente si può immaginare che l’aria sottostante spinga verso l’alto l’ala, mentre al di sopra di essa si genera un effetto di “risucchio”.

Come accennato in precedenza, la pressione non è davvero l’unica responsabile nell’insorgenza della portanza, anche la viscosità dell’aria è in grado di generare una parte di questa forza. Tuttavia, nel caso di un profilo alare il contributo della viscosità alla portanza è quasi sempre trascurabile. Per farvi un’idea più concreta in merito considerate che gli effetti viscosi nel caso appena analizzato sono minori dell’1% rispetto a quelli della pressione.

Dal profilo alare all’ala finita

In realtà, lo studio della portanza tramite un profilo alare può essere solo il punto di partenza di un ragionamento ben più complesso che prende in considerazione la tridimensionalità di un’ala. Infatti, la risposta di un profilo alare è assimilabile a quello di un’ala di apertura infinita, la quale si contrappone alla più realistica ala ad apertura finita.

La differenza sostanziale fra le due è che la presenza delle estremità nell’ala finita produce i cosiddetti vortici di estremità d’ala: questi vortici sono causati dal tentativo da parte dell’aria di passare dalla regione ad alta pressione dell’ala (sotto) a quella a bassa pressione (sopra) preferendo il percorso attorno alle estremità. Come conseguenza di ciò il flusso attorno all’ala finita diventa tridimensionale e la distribuzione della portanza lungo l’ala più complessa. Inoltre, sempre a causa dei vortici l’ala finita risulta meno efficiente nel produrre portanza rispetto al suo profilo alare.

Come avete potuto constatare voi stessi nell’articolo, parlare di portanza – o di fluidodinamica più in generale – porta le cose a complicarsi rapidamente e di conseguenza chiarire questi concetti cercando di svuotarli della loro complessità funziona fino ad un certo punto. Speriamo però di avervi dato perlomeno una buona idea di partenza sulla fisica che si cela dietro l’affascinante processo del volo.

Articolo a cura di Axel Baruscotti