La fatica nei componenti strutturali aerospaziali

La fatica nei componenti strutturali aerospaziali è uno dei guasti più frequenti e rilevanti nel settore aeronautico, correlato a sollecitazioni variabili e cicliche nel tempo che possono scaturire, ad esempio, per via dei carichi di pressurizzazione sulla fusoliera.
Tra i possibili tipi di guasto possiamo ricordare i seguenti:
- yielding;
- fretting;
- stress corrosion;
- buckling;
- creep;
- ductile rupture.
In particolare, ci si focalizzerà sulla fatica nei componenti: quel fenomeno che si presenta quando un componente è sottoposto a carichi ciclici, variabili nel tempo, che possono portare a rottura anche sotto carichi inferiori a quelli massimi ammissibili in condizioni statiche. È importante valutare come interagiscono tra loro i vari modi di cedimento di una struttura; ad esempio, il fretting (letteralmente “sfregamento”) si genera quando vi è moto relativo tra le superfici di contatto e accentua il danno a fatica causando una riduzione notevole della vita operativa del componente.
A seconda dei carichi e del numero di cicli operativi, si può distinguere:
- Fatica ad alti numeri di cicli HCF – High Cycle Fatigue, per numero di cicli maggiori di 10000;
- Fatica a bassi numeri di cicli LCF – Low Cycle Fatigue, per cicli inferiori a 10000;
- Fatica di corrosione;
- Fatica di impatto;
- Fatica termica, quando i carichi termici variano nel tempo;
- Fatica superficiale.
Tra le varie fenomenologie appena indicate, la fatica ad alti numeri di cicli è la più rilevante nei progetti strutturali, e componenti, aerospaziali.
La scoperta della fatica
Il fenomeno della fatica fu scoperto già dalla prima metà del 1800, quando William John Rankine (1820-1872), ingegnere e fisico scozzese, condusse i suoi primi studi su incidenti riguardanti gli assili ferroviari, intuendo che queste rotture fossero dovute all’iniziazione e alla propagazione di cricche.
Un fattore concomitante alla loro rottura era deputata alla presenza di variazioni geometriche nei componenti, in corrispondenza delle quali si poteva notare un’intensificazione dello stress.

https://it.wikipedia.org
Tuttavia, in quel periodo storico, data l’inadeguatezza degli strumenti a disposizione, non era possibile effettuare analisi microscopiche sui materiali danneggiati e per risolvere il problema i progettisti iniziarono ad adottare approcci di tipo fenomenologico.
August Wöhler, ingegnere tedesco pioniere degli studi metallurgici sulla fatica, costruì delle macchine per la sperimentazione a fatica dei componenti, fornendo un approccio statistico ed empirico sotto forma di diagrammi che si rivelarono molto utili per la progettazione a fatica: le curve di Wöhler.
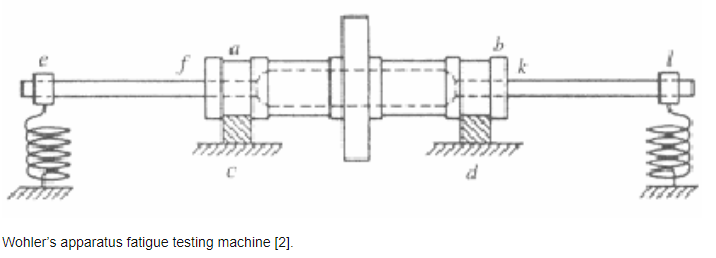
https://www.researchgate.net “Reliability and fatigue life evaluation of railway axles”, Meral Bayraktar
Con questa macchina l’ingegnere tedesco riuscì a simulare il carico sugli assili che, in un sistema di riferimento rotante solidale all’assile, oscilla tra un massimo ed un minimo di tensione (alternating stress), variando nel tempo in accordo con la velocità di rotazione imposta. Da queste considerazioni si può evincere che la tensione segua un andamento sinusoidale nel tempo.

http://tesi.cab.unipd.it “La fatica nei materiali metallici: dalla teoria alla pratica”, Luca Baiocchi
In statica si presuppone che un carico sia applicato in uno specifico punto e che la struttura sia sempre la stessa; immaginando che questa venga posta in rotazione, si ottengono delle tensioni variabili nel tempo. Questo concetto riassume la sostanziale differenza tra la statica e la fatica nei componenti, per cui i criteri di verifica strutturale, quali il criterio di Tresca oppure il criterio di Von Mises, non sono sufficienti a caratterizzare meccanicamente il componente, dal momento che la discriminante non è più la massima sollecitazione ammissibile, bensì la variazione di tensione.
Curve di Wöhler
I risultati ottenuti da Wöhler si presentano sotto forma di grafici e prendono il nome di curve di Wöhler, anche note come curve S-N.
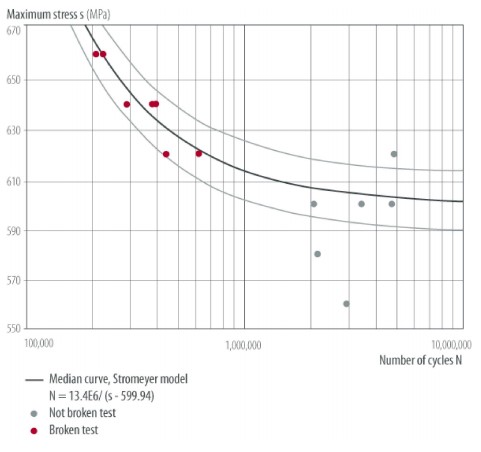
https://people.unica.it/
Sull’asse delle ascisse viene riportato il numero di cicli, sulle ordinate l’ampiezza della tensione, definita come segue:
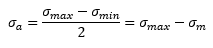
Nell’equazione sopra è possibile intuire facilmente che i termini si riferiscono alla tensione minima, la tensione massima e alla tensione media nella seconda uguaglianza; inoltre, nella figura sopra, le curve tendono a un asintoto orizzontale che rappresenta il cosiddetto limite di fatica, o limite di Wöhler, ossia quel valore di tensione al di sotto del quale non è possibile che si verifichi la rottura del componente. Convenzionalmente, esso si indica con il pedice “D” ed è quel valore raggiunto dopo 2 milioni di cicli.
I diagrammi introdotti possono essere studiati più agevolmente su scala logaritmica:

In questo caso, la tensione media è nulla, motivo per il quale il limite di fatica viene usualmente indicato con il pedice “D-1“, in cui -1 è il valore assunto dallo “Stress Ratio“, definito come:
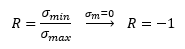
Sulle ordinate compare la tensione di rottura, con la quale si può identificare il primo “ginocchio” della curva, segnando il confine tra la fatica ad alti numeri di cicli e quella a bassi numeri di cicli. Da normativa, tale ginocchio viene posto in corrispondenza del 90% della tensione di rottura statica. La curva si costruisce conoscendo due punti e approssimandola ad una retta: il limite di fatica e la tensione di rottura, ossia due caratteristiche meccaniche del materiale.
Data la natura bi-logaritmica del diagramma, teoricamente la curva è esponenziale e quindi si può scrivere la relazione caratteristica:
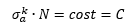
I parametri incogniti sono la costante C e l’esponente k che si possono ricavare una volta noti i due punti caratteristici della retta, risolvendo il seguente sistema:
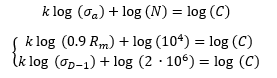
Generalmente, le curve di Wöhler si costruiscono con tensione media pari a zero. Nel caso in cui la tensione media fosse diversa da zero, le curve tenderebbero ad abbassarsi.

Se l’argomento riguardante la fatica nei componenti aerospaziali vi ha particolarmente interessato, vi suggeriamo di leggere il nostro articolo a riguardo del DH.106 Comet.
